संपूर्ण साखळीसाठी आणि साखळीच्या एका भागासाठी ओमचा नियम: सूत्र पर्याय, वर्णन आणि स्पष्टीकरण

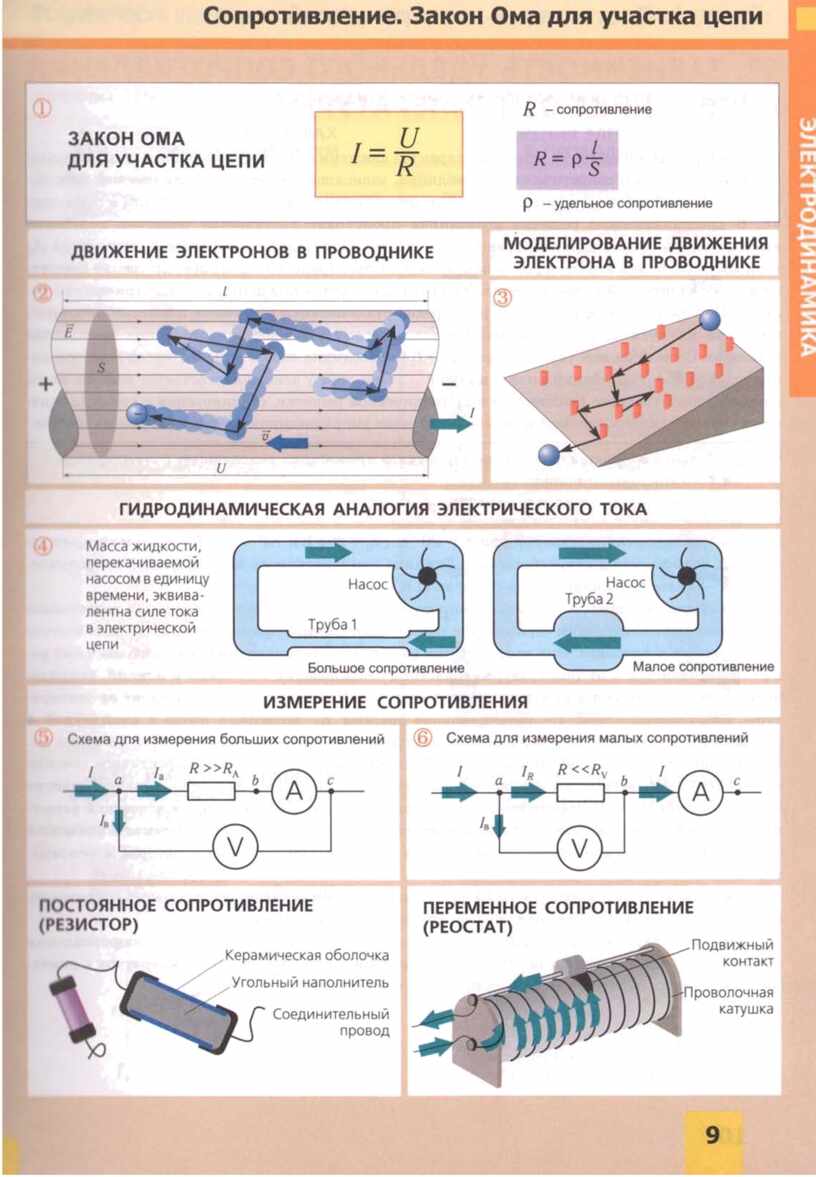
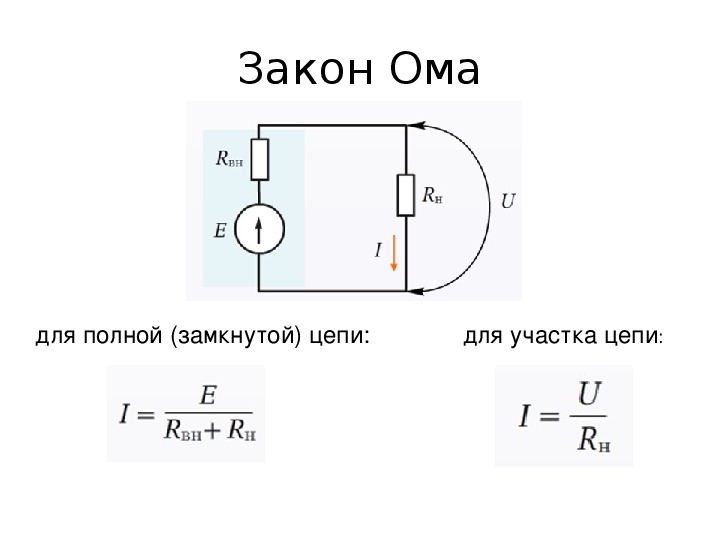
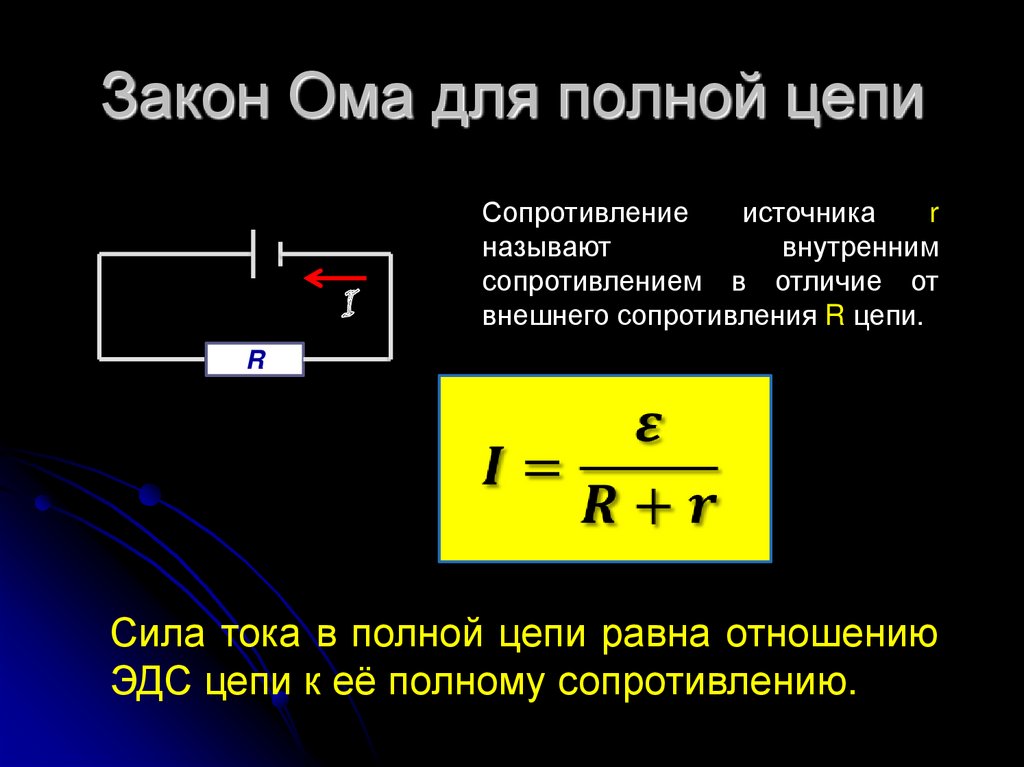
बंद सर्किटसाठी

बंद सर्किट म्हणजे बंद विद्युत कनेक्शन ज्याद्वारे विद्युत प्रवाह चालू होतो. जेव्हा मी वर्तुळाच्या एका टोकापासून दुस-या टोकापर्यंत धावत असतो तेव्हा एकमेकांशी जोडलेल्या आणि सर्किट पूर्ण करण्यासाठी तारांची मालिका असते तेव्हा ते एक बंद सर्किट असेल.

EMF (E) - व्होल्टमध्ये दर्शविले जाते आणि मोजले जाते आणि फॅराडेच्या कायद्यानुसार बॅटरी किंवा चुंबकीय शक्तीद्वारे व्युत्पन्न केलेल्या व्होल्टेजचा संदर्भ देते, जे सांगते की वेळ-बदलणारे चुंबकीय क्षेत्र विद्युत प्रवाह प्रवृत्त करेल.

नंतर: E = IR + Ir

E \u003d I (R + r)

I \u003d E / (R + r)

कुठे: r हा वर्तमान स्त्रोताचा प्रतिकार आहे.

ही अभिव्यक्ती बंद लूप सर्किट्सचा ओमचा नियम म्हणून ओळखली जाते.

विषम साखळी

विभक्त विभाग आणि पूर्ण इलेक्ट्रिकल सर्किट

विभाग किंवा संपूर्ण सर्किटला लागू केल्याप्रमाणे ओमचा नियम दोन गणना पर्यायांमध्ये विचारात घेतला जाऊ शकतो:

• वेगळा लहान विभाग. हे ईएमएफ स्त्रोताशिवाय सर्किटचा भाग आहे.
• एक किंवा अधिक विभागांचा समावेश असलेली संपूर्ण साखळी. यामध्ये स्वतःच्या अंतर्गत प्रतिकारासह EMF स्त्रोत देखील समाविष्ट आहे.

इलेक्ट्रिकल सर्किटच्या वर्तमान विभागाची गणना

या प्रकरणात, मूलभूत सूत्र I \u003d U/R लागू केले आहे, ज्यामध्ये I वर्तमान सामर्थ्य आहे, U व्होल्टेज आहे, R हा प्रतिकार आहे. त्यानुसार, कोणीही ओमच्या कायद्याचे सामान्यतः स्वीकारलेले स्पष्टीकरण तयार करू शकते:

हे सूत्रीकरण ग्राफिक डिझाइनमध्ये तथाकथित "कॅमोमाइल" वर सादर केलेल्या इतर अनेक सूत्रांसाठी आधार आहे. सेक्टर पी मध्ये - पॉवर निर्धारित केली जाते, सेक्टर I, U आणि R मध्ये - वर्तमान सामर्थ्य, व्होल्टेज आणि प्रतिकार यांच्याशी संबंधित क्रिया केल्या जातात.

प्रत्येक अभिव्यक्ती - मूलभूत आणि अतिरिक्त दोन्ही, आपल्याला सर्किटमध्ये वापरण्यासाठी हेतू असलेल्या घटकांच्या अचूक पॅरामीटर्सची गणना करण्यास अनुमती देते.

इलेक्ट्रिकल सर्किट्ससह काम करणारे विशेषज्ञ आकृतीमध्ये दर्शविलेल्या त्रिकोण पद्धतीचा वापर करून कोणत्याही पॅरामीटर्सचे द्रुत निर्धारण करतात.

गणनाने विभागातील घटकांना जोडणाऱ्या कंडक्टरचा प्रतिकार विचारात घेतला पाहिजे. ते वेगवेगळ्या सामग्रीपासून बनविलेले असल्याने, प्रत्येक बाबतीत हे पॅरामीटर भिन्न असेल.संपूर्ण सर्किट तयार करणे आवश्यक असल्यास, मुख्य सूत्र व्होल्टेज स्त्रोताच्या पॅरामीटर्ससह पूरक आहे, उदाहरणार्थ, बॅटरी.

संपूर्ण साखळीसाठी गणना पर्याय

संपूर्ण सर्किटमध्ये व्होल्टेज स्त्रोत (EMF) सह एकल संपूर्ण एकत्रित केलेले स्वतंत्र विभाग असतात. अशा प्रकारे, विभागांचा विद्यमान प्रतिकार कनेक्ट केलेल्या स्त्रोताच्या अंतर्गत प्रतिकाराने पूरक आहे. म्हणून, आधी चर्चा केलेली मुख्य व्याख्या खालीलप्रमाणे वाचली जाईल: I = U / (R + r). येथे, EMF स्त्रोताचा प्रतिरोधक निर्देशक (r) आधीच जोडला गेला आहे.

शुद्ध भौतिकशास्त्राच्या दृष्टिकोनातून, हे सूचक खूप लहान मूल्य मानले जाते. तथापि, सराव मध्ये, जटिल सर्किट्स आणि सर्किट्सची गणना करताना, तज्ञांना ते विचारात घेण्यास भाग पाडले जाते, कारण अतिरिक्त प्रतिकार कामाच्या अचूकतेवर परिणाम करतो. याव्यतिरिक्त, प्रत्येक स्त्रोताची रचना खूप विषम आहे, परिणामी, काही प्रकरणांमध्ये प्रतिकार उच्च दराने व्यक्त केला जाऊ शकतो.

वरील गणना डीसी सर्किट्सच्या संबंधात केली जाते. पर्यायी प्रवाहासह क्रिया आणि गणना वेगळ्या योजनेनुसार केली जातात.

व्हेरिएबलवर कायद्याचा प्रभाव

वैकल्पिक प्रवाहासह, सर्किटचा प्रतिकार तथाकथित प्रतिबाधा असेल, ज्यामध्ये सक्रिय प्रतिकार आणि प्रतिक्रियात्मक प्रतिरोधक भार असतो. हे प्रेरक गुणधर्म आणि साइनसॉइडल वर्तमान मूल्य असलेल्या घटकांच्या उपस्थितीमुळे आहे. व्होल्टेज देखील एक व्हेरिएबल आहे, त्याच्या स्वत: च्या स्विचिंग कायद्यानुसार कार्य करते.

म्हणून, ओमचा कायदा एसी सर्किट डिझाइन विशिष्ट प्रभाव लक्षात घेऊन गणना केली जाते: व्होल्टेजमधून विद्युत् प्रवाहाच्या विशालतेमध्ये अग्रगण्य किंवा मागे पडणे, तसेच सक्रिय आणि प्रतिक्रियाशील शक्तीची उपस्थिती.या बदल्यात, अभिक्रियामध्ये प्रेरक किंवा कॅपेसिटिव्ह घटक समाविष्ट असतात.

या सर्व घटना Z \u003d U / I किंवा Z \u003d R + J * (XL - XC) या सूत्राशी संबंधित असतील, ज्यामध्ये Z हा प्रतिबाधा आहे; आर - सक्रिय लोड; XL, XC - प्रेरक आणि कॅपेसिटिव्ह भार; J हा सुधारणा घटक आहे.

संपूर्ण सर्किटमध्ये EMF स्त्रोत

बंद सर्किटमध्ये विद्युत प्रवाहाच्या घटनेसाठी, या सर्किटमध्ये कमीतकमी एक विशेष घटक असणे आवश्यक आहे ज्यामध्ये त्याच्या ध्रुवांमधील शुल्क हस्तांतरित करण्याचे काम केले जाईल. या घटकामध्ये प्रभार वाहून नेणारी शक्ती विद्युत क्षेत्राविरुद्ध असे करतात, याचा अर्थ त्यांचा स्वभाव विद्युत्पेक्षा वेगळा असावा. म्हणून, अशा शक्तींना तृतीय-पक्ष म्हणतात.

तांदूळ. 1. भौतिकशास्त्रातील बाह्य शक्ती.

इलेक्ट्रिकल सर्किटचा एक घटक ज्यामध्ये बाह्य शक्ती विद्युत क्षेत्राच्या क्रियेवर शुल्क हस्तांतरित करण्यासाठी कार्य करतात त्याला वर्तमान स्त्रोत म्हणतात. बाह्य शक्तींचे परिमाण हे त्याचे मुख्य वैशिष्ट्य आहे. ते वैशिष्ट्यीकृत करण्यासाठी, एक विशेष उपाय सादर केला जातो - इलेक्ट्रोमोटिव्ह फोर्स (EMF), ते अक्षर $\mathscr{E}$ द्वारे दर्शविले जाते.

वर्तमान स्त्रोताच्या EMF चे मूल्य या शुल्काच्या मूल्यामध्ये शुल्क हस्तांतरणासाठी बाह्य शक्तींच्या गुणोत्तराच्या बरोबरीचे आहे:

$$\mathscr{E}={A_{st}\over q}$$

EMF चा अर्थ इलेक्ट्रिकल व्होल्टेजच्या अर्थाच्या अगदी जवळ असल्याने (आठवणे, व्होल्टेज हे विद्युत क्षेत्राद्वारे केलेल्या कार्याचे गुणोत्तर आहे जे या शुल्काच्या मूल्यापर्यंत चार्ज करते), तर EMF, व्होल्टेजप्रमाणे, मध्ये मोजले जाते. व्होल्ट:

$$1B={J\overCl}$$

वास्तविक वर्तमान स्त्रोताचे दुसरे सर्वात महत्वाचे विद्युत वैशिष्ट्य म्हणजे त्याचा अंतर्गत प्रतिकार.जेव्हा चार्जेस टर्मिनल्स दरम्यान हस्तांतरित केले जातात, तेव्हा ते EMF स्त्रोताच्या पदार्थाशी संवाद साधतात आणि म्हणूनच, विद्युत प्रवाहाचा स्त्रोत देखील काही प्रतिकार दर्शवतो. अंतर्गत प्रतिकार, सामान्य प्रतिकाराप्रमाणे, ओहममध्ये मोजला जातो, परंतु लहान लॅटिन अक्षर $r$ द्वारे दर्शविला जातो.

तांदूळ. 2. वर्तमान स्त्रोतांची उदाहरणे.

आर - विद्युत प्रतिकार

रेझिस्टन्स हा व्होल्टेजचा परस्पर आहे आणि त्याची तुलना वाहत्या पाण्यात शरीराला हालचाल करण्याच्या परिणामाशी करता येते. R चे एकक ओम आहे, जे कॅपिटल ग्रीक अक्षर ओमेगा द्वारे दर्शविले जाते.

रेसिप्रोकल ऑफ रेझिस्टन्स (1/R) ही चालकता म्हणून ओळखली जाते, जी सीमेन्स युनिट्समध्ये व्यक्त केलेल्या चार्ज घेण्याच्या ऑब्जेक्टची क्षमता मोजते.

वापरल्या जाणार्‍या भौमितीयदृष्ट्या स्वतंत्र प्रमाणाला प्रतिरोधकता म्हणतात आणि सामान्यतः ग्रीक चिन्ह r द्वारे दर्शविले जाते.

अतिरिक्त माहिती. ओमचा कायदा इलेक्ट्रिकल नेटवर्कच्या ऑपरेशनचे तीन महत्वाचे संकेतक स्थापित करण्यात मदत करतो, जे शक्तीची गणना सुलभ करते. हे डायोड, ट्रान्झिस्टर आणि यासारख्या घटकांसह एकतर्फी नेटवर्कवर लागू होत नाही. आणि हे नॉन-लिनियर एलिमेंट्सनाही लागू होत नाही, ज्यापैकी थायरिस्टर्स ही उदाहरणे आहेत, कारण या घटकांचे रेझिस्टन्स व्हॅल्यू वेगवेगळ्या दिलेल्या व्होल्टेज आणि करंटने बदलते.

उच्च फ्रिक्वेन्सीवर, वितरित वर्तन प्रबळ होते. खूप लांब पॉवर लाईन्सच्या बाबतीतही असेच घडते. 60 हर्ट्झ एवढी कमी वारंवारता असतानाही, 30 किमी सारख्या खूप लांब ट्रान्समिशन लाइनचे वितरीत स्वरूप असते.याचे मुख्य कारण म्हणजे सर्किट्समध्ये प्रसारित होणारे प्रभावी विद्युत सिग्नल हे इलेक्ट्रोमॅग्नेटिक लहरी आहेत, व्होल्ट आणि अँपिअर नसून, जे इलेक्ट्रोमॅग्नेटिक लहरीद्वारे संक्रमित होतात. कंडक्टर फक्त लाटांसाठी मार्गदर्शक म्हणून काम करतात. म्हणून, उदाहरणार्थ, एक समाक्षीय केबल Z = 75 ohms दर्शवेल, जरी त्याचा DC प्रतिकार नगण्य असेल.

ओमचा नियम हा विद्युत अभियांत्रिकीचा मूलभूत नियम आहे. यात सर्व इलेक्ट्रिकल सर्किट्स आणि इलेक्ट्रॉनिक घटकांमध्ये मोठ्या प्रमाणात व्यावहारिक अनुप्रयोग आहेत.

ओमच्या कायद्याच्या वापराची सर्वात सामान्य उदाहरणे:

1. इलेक्ट्रिक हीटरला वीज पुरवली जाते. हीटर कॉइलचा प्रतिकार आणि लागू केलेला व्होल्टेज लक्षात घेता, त्या हीटरला पुरवलेली शक्ती मोजली जाऊ शकते.
2. फ्यूजची निवड. ते संरक्षण घटक आहेत जे इलेक्ट्रॉनिक उपकरणांसह मालिकेत जोडलेले आहेत. फ्यूज/सीबी amps मध्ये रेट केले जातात. वर्तमान फ्यूज रेटिंग ओहमच्या नियमाचा वापर करून मोजली जाते.
3. इलेक्ट्रॉनिक उपकरणांची रचना. लॅपटॉप आणि मोबाईल फोन सारख्या इलेक्ट्रॉनिक उपकरणांना विशिष्ट वर्तमान रेटिंगसह DC पॉवर सप्लाय आवश्यक आहे. ठराविक मोबाइल फोनच्या बॅटरींना 0.7-1A आवश्यक असते. या घटकांमधून वाहणाऱ्या विद्युत् प्रवाहाचा दर नियंत्रित करण्यासाठी प्रतिरोधक वापरला जातो. ठराविक सर्किटमध्ये रेट केलेले प्रवाह मोजण्यासाठी ओहमचा नियम वापरला जातो.

एकेकाळी, ओमचे निष्कर्ष विजेच्या क्षेत्रातील नवीन संशोधनासाठी उत्प्रेरक बनले आणि आज त्यांचे महत्त्व गमावले नाही, कारण आधुनिक विद्युत अभियांत्रिकी त्यांच्यावर आधारित आहे. 1841 मध्ये, ओमला रॉयल सोसायटीचा सर्वोच्च सन्मान, कोपली पदक देण्यात आला आणि 1872 च्या सुरुवातीला "ओम" हा शब्द प्रतिकार एकक म्हणून ओळखला गेला.

डीसी सर्किटचा एकसमान नसलेला विभाग

विषम संरचनेत सर्किटचा असा विभाग असतो, जेथे कंडक्टर आणि घटकांव्यतिरिक्त, वर्तमान स्त्रोत असतो. या क्षेत्रातील एकूण वर्तमान शक्तीची गणना करताना त्याचा EMF विचारात घेणे आवश्यक आहे.

एक सूत्र आहे जे विषम साइटचे मुख्य पॅरामीटर्स आणि प्रक्रिया परिभाषित करते: q = q0 x n x V. त्याचे निर्देशक खालीलप्रमाणे आहेत:

• चार्जेस (q) हलवण्याच्या प्रक्रियेत, त्यांना एक विशिष्ट घनता प्राप्त होते. त्याची कार्यक्षमता वर्तमान सामर्थ्य आणि कंडक्टर (एस) च्या क्रॉस-सेक्शनल क्षेत्रावर अवलंबून असते.
• एका विशिष्ट एकाग्रता (n) च्या परिस्थितीत, एका कालावधीत हलविलेल्या युनिट शुल्कांची संख्या (q0) अचूकपणे सूचित करणे शक्य आहे.
• गणनेसाठी, कंडक्टरला सशर्तपणे काही व्हॉल्यूम (V) सह बेलनाकार विभाग मानले जाते.

कंडक्टरला बॅटरीशी जोडताना, नंतरचे काही वेळाने डिस्चार्ज केले जाईल. म्हणजेच, इलेक्ट्रॉनची हालचाल हळूहळू कमी होते आणि शेवटी, पूर्णपणे थांबते. हे कंडक्टरच्या आण्विक जाळीद्वारे सुलभ होते, जे एकमेकांशी आणि इतर घटकांसह इलेक्ट्रॉनच्या टक्करचा प्रतिकार करते. अशा प्रतिकारांवर मात करण्यासाठी, काही तृतीय-पक्ष शक्ती अतिरिक्तपणे लागू करणे आवश्यक आहे.

गणनेदरम्यान, ही शक्ती कुलॉम्बमध्ये जोडली जाते. याव्यतिरिक्त, युनिट चार्ज q 1ल्या बिंदूपासून 2रा पर्यंत हस्तांतरित करण्यासाठी, A1-2 किंवा फक्त A12 कार्य करणे आवश्यक असेल. या उद्देशासाठी, संभाव्य फरक (ϕ1 - ϕ2) तयार केला जातो. थेट वर्तमान स्त्रोताच्या कृती अंतर्गत, एक EMF उद्भवते, सर्किटच्या बाजूने शुल्क हलवते. एकूण ताणाच्या परिमाणात वर नमूद केलेल्या सर्व शक्तींचा समावेश असेल.

गणनामध्ये डीसी पुरवठ्याशी जोडणीची ध्रुवीयता विचारात घेणे आवश्यक आहे. जेव्हा टर्मिनल बदलले जातात, तेव्हा EMF देखील बदलेल, शुल्काची हालचाल वेगवान किंवा कमी करेल.

घटकांचे अनुक्रमिक आणि समांतर कनेक्शन

इलेक्ट्रिकल सर्किटच्या घटकांसाठी (सर्किटचा विभाग), एक वैशिष्ट्यपूर्ण क्षण म्हणजे मालिका किंवा समांतर कनेक्शन.

त्यानुसार, प्रत्येक प्रकारचे कनेक्शन वर्तमान प्रवाह आणि व्होल्टेज पुरवठ्याच्या भिन्न स्वरूपासह आहे. या खात्यावर, घटक समाविष्ट करण्याच्या पर्यायावर अवलंबून, ओमचा नियम देखील वेगवेगळ्या प्रकारे लागू केला जातो.

मालिका-कनेक्ट केलेल्या प्रतिरोधक घटकांची साखळी

मालिका कनेक्शन (दोन घटकांसह सर्किटचा विभाग) संदर्भात, शब्दरचना वापरली जाते:

• मी = मी₁ = मी₂ ;
• U = U₁ + U₂ ;
• R=R₁ + आर₂

हे फॉर्म्युलेशन स्पष्टपणे दाखवते की, मालिकेत जोडलेल्या प्रतिरोधक घटकांच्या संख्येकडे दुर्लक्ष करून, सर्किटच्या एका विभागात वाहणारा विद्युत् प्रवाह मूल्य बदलत नाही.

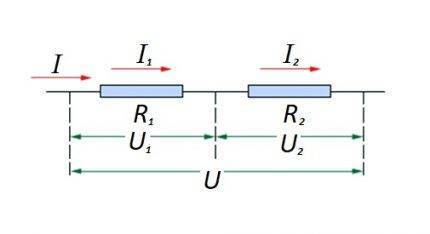सर्किट विभागातील प्रतिरोधक घटक एकमेकांशी मालिकेत जोडणे. या पर्यायाचा स्वतःचा गणना कायदा आहे. आकृतीमध्ये: I, I1, I2 - वर्तमान प्रवाह; आर 1, आर 2 - प्रतिरोधक घटक; U, U1, U2 - लागू व्होल्टेज

सर्किटच्या सक्रिय प्रतिरोधक घटकांवर लागू केलेल्या व्होल्टेजची रक्कम ही बेरीज आहे आणि EMF स्त्रोताच्या मूल्यापर्यंत जोडते.

या प्रकरणात, प्रत्येक वैयक्तिक घटकावरील व्होल्टेज आहे: Ux = I * Rx.

एकूण प्रतिकार सर्किटच्या सर्व प्रतिरोधक घटकांच्या मूल्यांची बेरीज मानला पाहिजे.

समांतर जोडलेल्या प्रतिरोधक घटकांची साखळी

जेव्हा प्रतिरोधक घटकांचे समांतर कनेक्शन असते तेव्हा जर्मन भौतिकशास्त्रज्ञ ओमच्या कायद्याच्या संदर्भात सूत्रीकरण योग्य मानले जाते:

• मी = मी₁ + मी₂ … ;
• U = U₁ = यू₂ … ;
• 1/R = 1/R₁ + 1 / आर₂ + …

समांतर आणि सीरियल कनेक्शन वापरले जातात तेव्हा "मिश्र" प्रकारचे सर्किट विभाग संकलित करण्याचे पर्याय वगळले जात नाहीत.

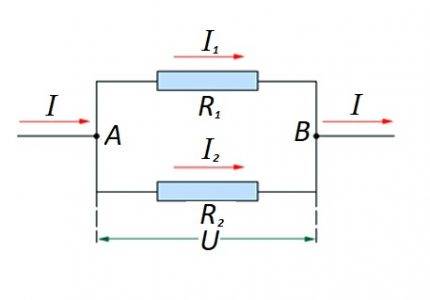सर्किट विभागातील प्रतिरोधक घटकांचे एकमेकांशी समांतर असलेले कनेक्शन. या पर्यायासाठी, स्वतःचा गणना कायदा लागू केला जातो. आकृतीमध्ये: I, I1, I2 - वर्तमान प्रवाह; आर 1, आर 2 - प्रतिरोधक घटक; यू - लागू व्होल्टेज; A, B - प्रवेश / निर्गमन बिंदू

अशा पर्यायांसाठी, गणना सहसा समांतर कनेक्शनच्या प्रतिरोधक रेटिंगच्या प्रारंभिक गणनाद्वारे केली जाते. त्यानंतर मालिकेत जोडलेल्या रेझिस्टरचे मूल्य निकालात जोडले जाते.

कायद्याचे अविभाज्य आणि विभेदक रूप

गणनासह वरील सर्व मुद्दे अशा परिस्थितींना लागू होतात जेव्हा “एकसंध” संरचनेचे कंडक्टर इलेक्ट्रिकल सर्किट्सचा भाग म्हणून वापरले जातात.

दरम्यान, सराव मध्ये, एखाद्याला अनेकदा योजनाबद्ध बांधकामाचा सामना करावा लागतो, जेथे कंडक्टरची रचना वेगवेगळ्या भागात बदलते. उदाहरणार्थ, मोठ्या क्रॉस सेक्शनच्या तारा वापरल्या जातात किंवा त्याउलट, वेगवेगळ्या सामग्रीच्या आधारे बनविलेल्या लहान.

अशा भिन्नता विचारात घेण्यासाठी, तथाकथित "विभेद-अविभाज्य ओम नियम" मध्ये भिन्नता आहे. अमर्यादपणे लहान कंडक्टरसाठी, वर्तमान घनता पातळीची तीव्रता आणि चालकता मूल्यावर अवलंबून गणना केली जाते.

विभेदक गणना अंतर्गत, सूत्र घेतले आहे: J = ό * E

अविभाज्य गणनेसाठी, अनुक्रमे, सूत्रीकरण: I * R = φ1 - φ2 + έ

तथापि, ही उदाहरणे उच्च गणिताच्या शाळेच्या अगदी जवळ आहेत आणि प्रत्यक्षात साध्या इलेक्ट्रिशियनच्या वास्तविक व्यवहारात वापरली जात नाहीत.

वर्तमान आणि प्रतिकार समजून घेणे

चला विद्युत प्रवाहाच्या संकल्पनेपासून सुरुवात करूया.थोडक्यात, धातूंच्या संबंधात विद्युत प्रवाह म्हणजे इलेक्ट्रॉनची निर्देशित हालचाल - नकारात्मक चार्ज केलेले कण. ते सहसा लहान मंडळे म्हणून दर्शविले जातात. शांत स्थितीत, ते यादृच्छिकपणे फिरतात, सतत त्यांची दिशा बदलतात. काही विशिष्ट परिस्थितींमध्ये - संभाव्य फरकाचे स्वरूप - हे कण काही दिशेने एक विशिष्ट हालचाल सुरू करतात. ही हालचाल म्हणजे विद्युत प्रवाह.

हे स्पष्ट करण्यासाठी, आम्ही इलेक्ट्रॉनची तुलना एखाद्या विमानात सांडलेल्या पाण्याशी करू शकतो. जोपर्यंत विमान स्थिर आहे, तोपर्यंत पाणी हलत नाही. परंतु, उतार दिसू लागताच (संभाव्य फरक निर्माण झाला), पाणी हलू लागले. इलेक्ट्रॉनच्या बाबतीतही असेच आहे.

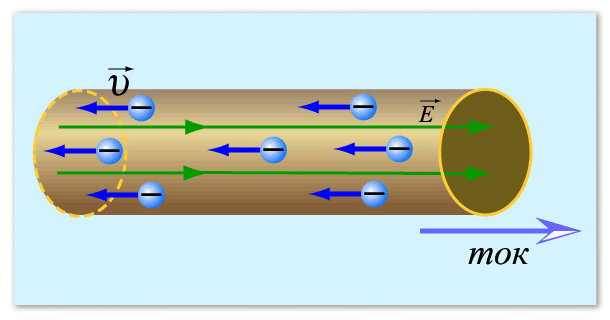
अशा प्रकारे विद्युत प्रवाहाची कल्पना करता येते

आता आपल्याला हे समजून घेणे आवश्यक आहे की प्रतिरोध म्हणजे काय आणि त्यांना वर्तमान शक्तीसह अभिप्राय का आहे: प्रतिरोध जितका जास्त असेल तितका प्रवाह कमी असेल. तुम्हाला माहिती आहे की, इलेक्ट्रॉन कंडक्टरमधून फिरतात. सामान्यत: या धातूच्या तारा असतात, कारण धातूंमध्ये वीज चालवण्याची क्षमता चांगली असते. आपल्याला माहित आहे की धातूमध्ये दाट क्रिस्टल जाळी आहे: बरेच कण जे जवळचे आणि एकमेकांशी जोडलेले आहेत. इलेक्ट्रॉन्स, धातूच्या अणूंमध्ये त्यांचा मार्ग बनवतात, त्यांच्याशी आदळतात, ज्यामुळे त्यांना हालचाल करणे कठीण होते. हे कंडक्टरचा प्रतिकार दर्शविण्यास मदत करते. आता हे स्पष्ट झाले आहे की प्रतिकार जितका जास्त असेल तितकी वर्तमान ताकद कमी का - अधिक कण, इलेक्ट्रॉनसाठी मार्गावर मात करणे अधिक कठीण आहे, ते ते अधिक हळू करतात. यावर तोडगा निघालेला दिसतो.

जर तुम्हाला या अवलंबित्वाची प्रायोगिकरित्या चाचणी करायची इच्छा असेल, तर व्हेरिएबल रेझिस्टर शोधा, मालिकेत रेझिस्टर कनेक्ट करा - अँमीटर - वर्तमान स्त्रोत (बॅटरी).सर्किटमध्ये एक स्विच घालणे देखील इष्ट आहे - एक सामान्य टॉगल स्विच.

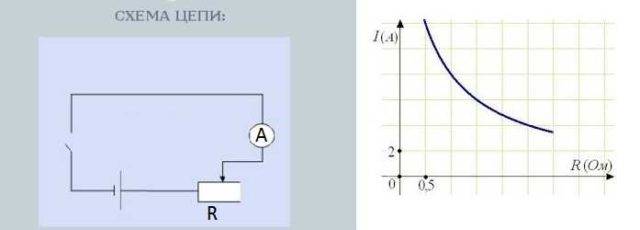
प्रतिकारावरील विद्युत् प्रवाहाच्या अवलंबनाची चाचणी करण्यासाठी सर्किट

रेझिस्टर नॉब फिरवल्याने रेझिस्टन्स बदलतो. त्याच वेळी, अॅमीटरवरील रीडिंग, जे वर्तमान ताकद मोजते, देखील बदलते. शिवाय, प्रतिकार जितका जास्त असेल तितका बाण कमी होईल - कमी प्रवाह. प्रतिकार जितका कमी असेल तितका बाण विचलित होईल - वर्तमान जास्त आहे.

रेझिस्टन्सवर करंटचे अवलंबित्व जवळजवळ रेषीय असते, म्हणजेच ते आलेखावर जवळजवळ सरळ रेषा म्हणून प्रतिबिंबित होते. जवळजवळ का - यावर स्वतंत्रपणे चर्चा केली पाहिजे, परंतु ही दुसरी कथा आहे.

पर्यायी प्रवाहासाठी ओमचा नियम

एसी सर्किट्सची गणना करताना, प्रतिकार संकल्पनेऐवजी, "प्रतिबाधा" ची संकल्पना सादर केली जाते. प्रतिबाधा Z अक्षराने दर्शविली जाते, त्यात लोड R चे सक्रिय प्रतिकार समाविष्ट आहे_a आणि प्रतिक्रिया X (किंवा आर_आर). हे सायनसॉइडल करंटच्या आकारामुळे (आणि इतर कोणत्याही स्वरूपाचे प्रवाह) आणि प्रेरक घटकांचे पॅरामीटर्स, तसेच स्विचिंग कायद्यांमुळे आहे:

1. प्रेरक सर्किटमधील विद्युत् प्रवाह त्वरित बदलू शकत नाही.
2. कॅपेसिटन्स असलेल्या सर्किटमधील व्होल्टेज त्वरित बदलू शकत नाही.

अशा प्रकारे, विद्युत् प्रवाह मागे पडण्यास किंवा व्होल्टेजचे नेतृत्व करण्यास सुरवात करतो आणि उघड शक्ती सक्रिय आणि प्रतिक्रियाशील मध्ये विभागली जाते.

U=I/Z

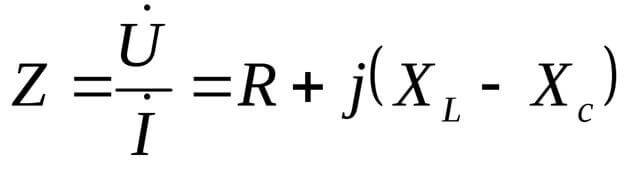
एक्स_एल आणि एक्स_सी लोडचे प्रतिक्रियाशील घटक आहेत.

या संदर्भात, cosФ मूल्य सादर केले आहे:

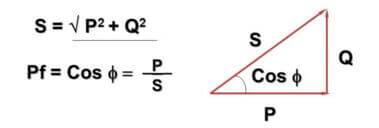
येथे - क्यू - पर्यायी विद्युत् प्रवाह आणि प्रेरक-कॅपॅसिटिव्ह घटकांमुळे प्रतिक्रियाशील शक्ती, P - सक्रिय शक्ती (सक्रिय घटकांमध्ये विसर्जित), S - स्पष्ट शक्ती, cosФ - पॉवर फॅक्टर.

तुमच्या लक्षात आले असेल की सूत्र आणि त्याचे प्रतिनिधित्व पायथागोरियन प्रमेयाला छेदतात. हे खरे आहे आणि कोन Ф लोडचा प्रतिक्रियाशील घटक किती मोठा आहे यावर अवलंबून असतो - ते जितके मोठे असेल तितके मोठे असेल.सराव मध्ये, हे या वस्तुस्थितीकडे नेत आहे की नेटवर्कमध्ये प्रत्यक्षात वाहणारा प्रवाह घरगुती मीटरने विचारात घेतलेल्यापेक्षा जास्त आहे, तर एंटरप्राइजेस पूर्ण शक्तीसाठी पैसे देतात.

या प्रकरणात, प्रतिकार जटिल स्वरूपात सादर केला जातो:

येथे j हे काल्पनिक एकक आहे, जे समीकरणांच्या जटिल स्वरूपासाठी वैशिष्ट्यपूर्ण आहे. कमी सामान्यतः i म्हणून संबोधले जाते, परंतु विद्युत अभियांत्रिकीमध्ये, पर्यायी प्रवाहाचे प्रभावी मूल्य देखील सूचित केले जाते, म्हणून, गोंधळात पडू नये म्हणून, j वापरणे चांगले आहे.

काल्पनिक एकक √-1 आहे. हे तार्किक आहे की स्क्वेअरिंग करताना अशी कोणतीही संख्या नाही, ज्यामुळे "-1" चे नकारात्मक परिणाम होऊ शकतात.

जेव्हा ओमचा नियम होतो

आदर्श परिस्थिती निर्माण करणे सोपे नाही. शुद्ध कंडक्टरमध्येही, विद्युत प्रतिरोध तापमानानुसार बदलतो. त्याची घट क्रिस्टल जाळीच्या रेणूंची क्रिया कमी करते, जे विनामूल्य शुल्काची हालचाल सुलभ करते. "फ्रीझिंग" च्या विशिष्ट स्तरावर सुपरकंडक्टिव्हिटीचा प्रभाव उद्भवतो. गरम केल्यावर उलट परिणाम (वाहकता बिघडणे) दिसून येते.

त्याच वेळी, इलेक्ट्रोलाइट्स, धातू आणि विशिष्ट प्रकारचे सिरेमिक वर्तमान घनतेकडे दुर्लक्ष करून विद्युत प्रतिरोध टिकवून ठेवतात. विशिष्ट तापमान व्यवस्था राखताना पॅरामीटर्सची स्थिरता अतिरिक्त सुधारणांशिवाय ओमच्या कायद्याची सूत्रे लागू करणे शक्य करते.

सेमीकंडक्टर सामग्री आणि वायू वेगवेगळ्या विद्युत प्रतिरोधकतेद्वारे दर्शविले जातात. हे पॅरामीटर नियंत्रण व्हॉल्यूममधील वर्तमान तीव्रतेमुळे लक्षणीयरीत्या प्रभावित होते. कार्यप्रदर्शन वैशिष्ट्यांची गणना करण्यासाठी, विशेष गणना पद्धती लागू करणे आवश्यक आहे.

पर्यायी प्रवाहाचा विचार केल्यास, गणना पद्धत दुरुस्त केली जाते.या प्रकरणात, प्रतिक्रियाशील घटकांची उपस्थिती विचारात घ्यावी लागेल. प्रतिकाराच्या प्रतिरोधक स्वरूपासह, ओमच्या कायद्याच्या सूत्रांवर आधारित विचारात घेतलेली गणना तंत्रज्ञान लागू करणे शक्य आहे.

किर्चहॉफचे कायदे.

वितरण
इलेक्ट्रिकल सर्किटच्या शाखांमधील प्रवाह
किर्चहॉफच्या पहिल्या कायद्याचे पालन करतो,
आणि विभागांवर ताणांचे वितरण
चेन किर्चॉफच्या दुसऱ्या कायद्याचे पालन करते.

किर्चहॉफचे कायदे
सोबत ओमचे नियम मुख्य आहेत
इलेक्ट्रिकल सर्किट्सच्या सिद्धांतामध्ये.

पहिला
किर्चहॉफचा कायदा:

बीजगणितीय
नोडमधील प्रवाहांची बेरीज शून्य आहे:

_i
= 0 (19)

कुठे
i
दिलेल्या नोडवर एकत्रित होणाऱ्या शाखांची संख्या आहे.

म्हणजे, बेरीज
शाखांमधील प्रवाहांपर्यंत विस्तारते,
जे विचारात एकत्र होतात
नोड

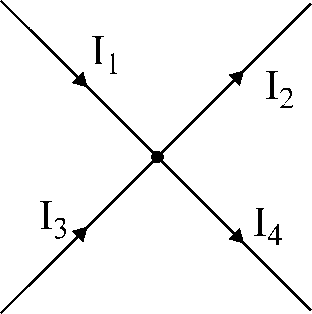
अंजीर.17. चित्रण
किर्चॉफच्या पहिल्या कायद्याला.

क्रमांक
पहिल्यानुसार संकलित केलेली समीकरणे
किर्चहॉफचा कायदा सूत्राद्वारे निर्धारित केला जातो:

नुप
= Nu
– 1,

कुठे
नू
विचारात घेतलेल्या साखळीतील नोड्सची संख्या आहे.

मध्ये प्रवाहांची चिन्हे
निवडलेली समीकरणे विचारात घेतली जातात
सकारात्मक दिशा. येथे चिन्हे
प्रवाह समान असल्यास प्रवाह समान असतात
याच्याशी संबंधित
नोड

उदाहरणार्थ,
अंजीर 17 मध्ये दर्शविलेल्या नोडसाठी:
आम्ही नोडकडे वाहणाऱ्या प्रवाहांना चिन्हे नियुक्त करतो
"+", आणि नोडमधून वाहणाऱ्या प्रवाहांकडे - चिन्हे
«-».

मग समीकरण
Kirchhoff च्या पहिल्या कायद्यानुसार, ते लिहिले जाईल
त्यामुळे:

आय₁
- आय₂
+ मी₃
- आय₄
= 0.

समीकरणे
किर्चहॉफच्या पहिल्या कायद्यानुसार संकलित,
नोड्स म्हणतात.

या
कायदा नोडमध्ये हे तथ्य व्यक्त करतो
इलेक्ट्रिक चार्ज जमा होत नाही
आणि सेवन केले जात नाही. विजेचे प्रमाण
साइटवर येणारे शुल्क बेरजेइतके आहे
नोडला एकसारखे सोडून शुल्क
समान कालावधी.

दुसरा
किर्चहॉफचा कायदा:

बीजगणितीय
emf ची बेरीज कोणत्याही बंद सर्किटमध्ये
साखळी फॉल्सच्या बीजगणितीय बेरजेइतकी असते
या सर्किटच्या घटकांवर व्होल्टेज:

Ui
= 
इ.इ

IiRi = Ei(20)

कुठे
i
- घटक क्रमांक (प्रतिकार किंवा
व्होल्टेज स्त्रोत) विचारात घेतले
समोच्च

** संख्या
दुसऱ्यानुसार संकलित केलेली समीकरणे
किर्चहॉफचा कायदा सूत्राद्वारे निर्धारित केला जातो:

नुप
= Nb
- नु
+ 1 – Ned.s.

कुठे
Nb
- इलेक्ट्रिकल सर्किटच्या शाखांची संख्या;

नू
- नोड्सची संख्या;

Ned.s.
आदर्श emf स्त्रोतांची संख्या आहे.

अंजीर.18. चित्रण
किर्चहॉफच्या दुसऱ्या कायद्याला.

च्या साठी,
दुसरा कायदा योग्यरित्या लिहिण्यासाठी
दिलेल्या समोच्च साठी Kirchhoff, खालीलप्रमाणे
खालील नियमांचे पालन करा:

1. स्वैरपणे
   समोच्च बायपासची दिशा निवडा,
   उदाहरणार्थ, घड्याळाच्या दिशेने (चित्र 18).

2. emf
   आणि व्होल्टेज थेंब जे जुळतात
   निवडलेल्या दिशेने दिशेने
   सह अभिव्यक्तीमध्ये बायपास लिहिलेले आहेत
   चिन्ह "+"; जर e.f.s. आणि व्होल्टेज ड्रॉप
   दिशा जुळत नाही
   समोच्च, नंतर ते चिन्हाच्या आधी आहेत
   «-».

उदाहरणार्थ,
अंजीर 18 च्या समोच्च साठी, Kirchhoff दुसरा कायदा
खालीलप्रमाणे लिहिले जाईल:

यू₁
- यू₂
+ U₃
=ई₁
- ई₃
- ई₄
(21)

समीकरण (20) असू शकते
असे पुन्हा लिहा:

 (Ui
- Ei)
= 0 (22)

कुठे
(यू
- ई)
- शाखेवर ताण.

परिणामी,
किर्चॉफचा दुसरा कायदा तयार केला जाऊ शकतो
खालील प्रकारे:

बीजगणितीय
कोणत्याही शाखांवरील व्होल्टेजची बेरीज
बंद लूप शून्य आहे.

संभाव्य
आधी चर्चा केलेली आकृती काम करते
दुसऱ्याचे ग्राफिकल व्याख्या
किर्चॉफचा कायदा.

कार्य क्रमांक १.

एटी
अंजीर 1 मधील सर्किटला विद्युत प्रवाह I दिलेला आहे₁
मी आणि₃,
प्रतिकार आणि emf प्रवाह निश्चित करा
आय₄,
आय₅,
आय₆
; बिंदूंमधील व्होल्टेज a
आणि ब
जर मी₁
= 10mA,
आय₃
= -20 एमए,
आर₄
= 5kOhm,
इ₅
= 20B,
आर₅
= 3kOhm,
इ₆
= 40B,
आर₆
= 2kOhm.

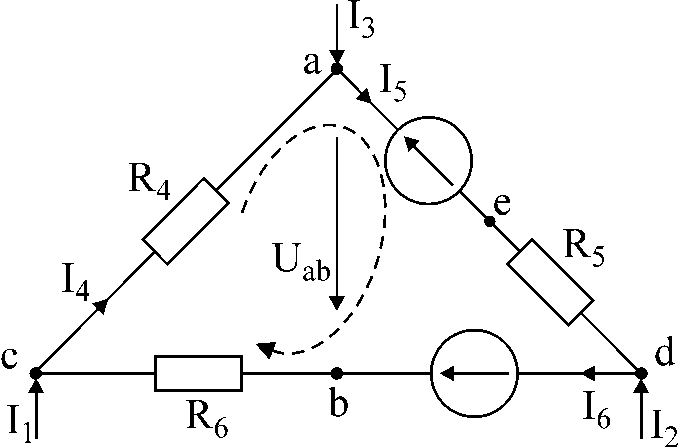
आकृती क्रं 1

उपाय:

1. दिलेल्या साठी
   समोच्च, त्यानुसार आम्ही दोन समीकरणे तयार करतो
   Kirchhoff चा पहिला कायदा आणि एक - त्यानुसार
   दुसरा समोच्च दिशा
   बाणाने सूचित केले आहे.

एटी
समाधानाच्या परिणामी आम्हाला मिळते: I₆
= 0; आय₄
= 10mA;
आय₅
= -10mA

1. विचारा
   बिंदूंमधील व्होल्टेज दिशा
   a
   आणि ब
   बिंदू "a" पासून
   "b" बिंदू करण्यासाठी
   - यू_ab.
   हे व्होल्टेज समीकरणावरून शोधता येते
   किर्चहॉफचा दुसरा कायदा:

आय₄आर₄
+ U_ab
+ मी₆आर₆
= 0

यू_ab
= - 50V.

कार्य क्रमांक 2.

च्या साठी
आकृती 2 मधील आकृतीनुसार समीकरणे काढा
Kirchhoff च्या कायदे आणि अज्ञात निर्धारित
गुण

दिले:
आय₁
= 20mA;
आय₂
= 10mA

आर₁
= 5kOhm,
आर₃
= 4kOhm,
आर₄
= 6kOhm,
आर₅
= 2kOhm,
आर₆
= 4kΩ.

अंजीर.2

उपाय:

नोड्सची संख्या
समीकरणे - 3, समोच्च समीकरणांची संख्या
– 1.

लक्षात ठेवा!
दुसऱ्या नुसार समीकरण संकलित करताना
Kirchhoff च्या नियम, आम्ही समोच्च निवडा, मध्ये
ज्यामध्ये वर्तमान स्त्रोतांचा समावेश नाही.
समोच्चची दिशा आकृतीमध्ये दर्शविली आहे.

एटी
या सर्किटचे, शाखांचे प्रवाह I₁
मी आणि₂.
अज्ञात
प्रवाह
आय₃,
आय₄,
आय₅,
आय₆.

ठरवत आहे
प्रणाली, आम्हाला मिळते: I₃
= 13.75 एमए;
आय₄
= -3.75mA;
आय₅
= 6.25mA;
आय₆
= 16.25mA.

मूलभूत संकल्पना

जेव्हा क्लोज सर्किट इलेक्ट्रॉन्सना सर्किटमधील उच्च क्षमतेपासून खालच्या क्षमतेकडे जाण्यास अनुमती देते तेव्हा विद्युत प्रवाह वाहतो. दुस-या शब्दात, विद्युत् प्रवाहाला इलेक्ट्रॉन्सच्या स्त्रोताची आवश्यकता असते ज्यामध्ये त्यांना गतिमान करण्यासाठी ऊर्जा असते, तसेच त्यांच्या नकारात्मक शुल्काच्या परताव्याच्या बिंदूची आवश्यकता असते, जे त्यांच्या कमतरतेद्वारे वैशिष्ट्यीकृत आहे. भौतिक घटना म्हणून, सर्किटमधील विद्युत् प्रवाह तीन मूलभूत प्रमाणांद्वारे दर्शविला जातो:

• विद्युतदाब;
• वर्तमान शक्ती;
• कंडक्टरचा प्रतिकार ज्याद्वारे इलेक्ट्रॉन हलतात.

सामर्थ्य आणि तणाव

वर्तमान सामर्थ्य (I, Amperes मध्ये मोजले जाते) म्हणजे सर्किटमधील प्रति युनिट वेळेच्या एका ठिकाणामधून फिरणारे इलेक्ट्रॉन (चार्ज) चे प्रमाण.दुसऱ्या शब्दांत, मोजमाप I हे गतीतील इलेक्ट्रॉनच्या संख्येचे निर्धारण आहे

हे समजून घेणे महत्त्वाचे आहे की हा शब्द फक्त हालचालींचा संदर्भ देतो: स्थिर शुल्क, उदाहरणार्थ, कनेक्ट न केलेल्या बॅटरीच्या टर्मिनल्सवर, I चे मोजण्यायोग्य मूल्य नसते. एका दिशेने वाहणाऱ्या विद्युत् प्रवाहाला थेट (DC) म्हणतात आणि वेळोवेळी दिशा बदलण्याला अल्टरनेटिंग (AC) म्हणतात. व्होल्टेज हे दाबासारख्या घटनेद्वारे किंवा गुरुत्वाकर्षणाच्या प्रभावाखाली असलेल्या वस्तूंच्या संभाव्य ऊर्जेमध्ये फरक म्हणून स्पष्ट केले जाऊ शकते.

हा असंतुलन निर्माण करण्यासाठी, आपण प्रथम ऊर्जा खर्च करणे आवश्यक आहे, जी योग्य परिस्थितीत गतीने साकार होईल. उदाहरणार्थ, उंचीवरून लोड पडल्यावर, ते उचलण्याचे काम केले जाते, गॅल्व्हॅनिक बॅटरीमध्ये, टर्मिनल्समधील संभाव्य फरक रासायनिक उर्जेच्या रूपांतरणामुळे तयार होतो, जनरेटरमध्ये - एक्सपोजरच्या परिणामी एक इलेक्ट्रोमॅग्नेटिक फील्ड

दबाव यासारख्या घटनेद्वारे किंवा गुरुत्वाकर्षणाच्या प्रभावाखाली असलेल्या वस्तूंच्या संभाव्य ऊर्जेमध्ये फरक म्हणून तणाव दर्शविला जाऊ शकतो. हा असंतुलन निर्माण करण्यासाठी, आपण प्रथम ऊर्जा खर्च करणे आवश्यक आहे, जी योग्य परिस्थितीत गतीने साकार होईल. उदाहरणार्थ, उंचावरून भार पडल्यावर, तो उचलण्याचे काम लक्षात येते, गॅल्व्हॅनिक बॅटरीमध्ये टर्मिनल्समधील संभाव्य फरक रासायनिक ऊर्जेच्या रूपांतरणामुळे तयार होतो, जनरेटरमध्ये - एखाद्याच्या प्रदर्शनाच्या परिणामी. इलेक्ट्रोमॅग्नेटिक फील्ड.

कंडक्टर प्रतिकार

सामान्य कंडक्टर कितीही चांगला असला तरीही, तो इलेक्ट्रॉनला त्यांच्या हालचालींना काही प्रतिकार केल्याशिवाय कधीही जाऊ देत नाही.यांत्रिक घर्षणाचा अॅनालॉग म्हणून प्रतिकार मानणे शक्य आहे, जरी ही तुलना परिपूर्ण होणार नाही. जेव्हा विद्युत् प्रवाह कंडक्टरमधून वाहतो तेव्हा काही संभाव्य फरक उष्णतेमध्ये रूपांतरित होतो, त्यामुळे रेझिस्टरमध्ये नेहमी व्होल्टेज ड्रॉप असेल. इलेक्ट्रिक हीटर्स, हेअर ड्रायर आणि इतर तत्सम उपकरणे केवळ उष्णतेच्या स्वरूपात विद्युत उर्जा नष्ट करण्यासाठी डिझाइन केलेली आहेत.

सरलीकृत प्रतिकार (R म्हणून दर्शविलेले) हे सर्किटमध्ये इलेक्ट्रॉनचा प्रवाह किती मंद आहे याचे मोजमाप आहे. हे ओममध्ये मोजले जाते. रेझिस्टर किंवा इतर घटकांची चालकता दोन गुणधर्मांद्वारे निर्धारित केली जाते:

• भूमिती;
• साहित्य

हायड्रॉलिक सादृश्यातून स्पष्ट केल्याप्रमाणे, आकार अत्यंत महत्त्वाचा आहे: लहान आणि रुंद पाईपमधून पाणी ढकलण्यापेक्षा लांब आणि अरुंद पाईपमधून पाणी ढकलणे खूप कठीण आहे. साहित्य निर्णायक भूमिका बजावते. उदाहरणार्थ, तांब्याच्या तारेमध्ये इलेक्ट्रॉन मुक्तपणे फिरू शकतात, परंतु त्यांच्या आकाराकडे दुर्लक्ष करून रबरसारख्या इन्सुलेटरमधून अजिबात वाहू शकत नाहीत. भूमिती आणि सामग्री व्यतिरिक्त, चालकता प्रभावित करणारे इतर घटक आहेत.

ओमच्या कायद्याचे स्पष्टीकरण

शुल्काची हालचाल सुनिश्चित करण्यासाठी, आपल्याला सर्किट बंद करणे आवश्यक आहे. अतिरिक्त शक्तीच्या अनुपस्थितीत, वर्तमान दीर्घकाळ अस्तित्वात राहू शकत नाही. संभाव्यता पटकन समान होईल. सर्किटचे ऑपरेटिंग मोड राखण्यासाठी, अतिरिक्त स्त्रोत (जनरेटर, बॅटरी) आवश्यक आहे.

संपूर्ण सर्किटमध्ये सर्व घटकांचा एकूण विद्युत प्रतिकार असेल. अचूक गणनेसाठी, कंडक्टरमधील नुकसान, प्रतिरोधक घटक आणि उर्जा स्त्रोत विचारात घेतले जातात.

विशिष्ट वर्तमान शक्तीसाठी किती व्होल्टेज लागू करणे आवश्यक आहे हे सूत्राद्वारे मोजले जाते:

U=I*R.

त्याचप्रमाणे, विचारात घेतलेल्या संबंधांच्या मदतीने, सर्किटचे इतर पॅरामीटर्स निर्धारित केले जातात.

समांतर आणि सीरियल कनेक्शन

इलेक्ट्रिकमध्ये, घटक एकतर मालिकेत जोडलेले असतात - एकामागून एक, किंवा समांतर - हे असे होते जेव्हा अनेक इनपुट एका बिंदूशी जोडलेले असतात आणि त्याच घटकांचे आउटपुट दुसर्याशी जोडलेले असतात.

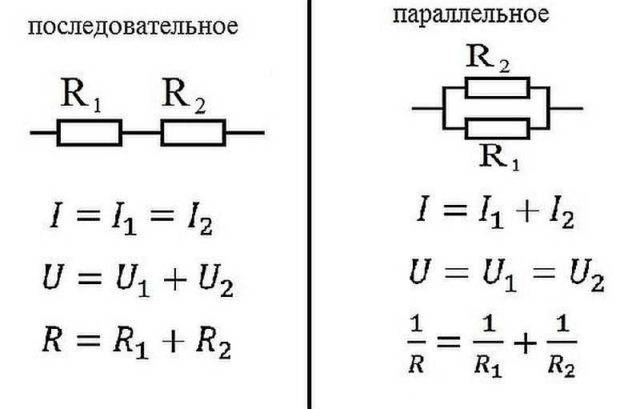
समांतर आणि मालिका कनेक्शनसाठी ओमचा नियम

सीरियल कनेक्शन

या प्रकरणांसाठी ओमचा कायदा कसा कार्य करतो? मालिकेत जोडलेले असताना, घटकांच्या साखळीतून वाहणारा विद्युत् प्रवाह सारखाच असेल. मालिकेत जोडलेल्या घटकांसह सर्किटच्या विभागातील व्होल्टेजची गणना प्रत्येक विभागातील व्होल्टेजची बेरीज म्हणून केली जाते. हे कसे स्पष्ट केले जाऊ शकते? एखाद्या घटकाद्वारे विद्युत प्रवाहाचा प्रवाह म्हणजे चार्जचा काही भाग त्याच्या एका भागातून दुसर्‍या भागात स्थानांतरित करणे. म्हणजे, काही काम आहे. या कामाचे मोठेपणा तणाव आहे. हा तणावाचा भौतिक अर्थ आहे. हे स्पष्ट असल्यास, आम्ही पुढे जाऊ.

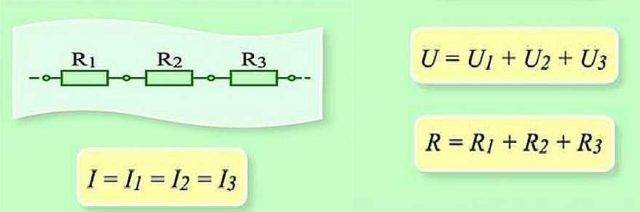
सर्किटच्या या विभागाचे सीरियल कनेक्शन आणि पॅरामीटर्स

मालिकेत कनेक्ट केल्यावर, प्रत्येक घटकाद्वारे चार्ज बदलणे आवश्यक आहे. आणि प्रत्येक घटकावर, हे कामाचे एक विशिष्ट "खंड" आहे. आणि साखळीच्या संपूर्ण विभागावरील कामाचे प्रमाण शोधण्यासाठी, आपल्याला प्रत्येक घटकावरील कार्य जोडण्याची आवश्यकता आहे. तर असे दिसून येते की एकूण व्होल्टेज ही प्रत्येक घटकावरील व्होल्टेजची बेरीज आहे.

त्याच प्रकारे - जोडणीच्या मदतीने - सर्किट विभागाचा एकूण प्रतिकार देखील आढळतो. आपण त्याची कल्पना कशी करू शकता? घटकांच्या साखळीतून वाहणारा विद्युत् प्रवाह क्रमाने सर्व प्रतिकारांवर मात करतो. एक एक करून. म्हणजेच, त्याने मात केलेला प्रतिकार शोधण्यासाठी, प्रतिकारांची भर घालणे आवश्यक आहे. कमी-जास्त असे.गणितीय व्युत्पत्ती अधिक क्लिष्ट आहे, आणि या कायद्याची यंत्रणा समजून घेणे सोपे आहे.

समांतर कनेक्शन

समांतर कनेक्शन म्हणजे जेव्हा कंडक्टर / घटकांची सुरुवात एका बिंदूवर एकत्र होते आणि दुसर्‍या ठिकाणी त्यांचे टोक जोडलेले असतात. आम्ही या प्रकारच्या संयुगांसाठी वैध कायदे स्पष्ट करण्याचा प्रयत्न करू. चला वर्तमानापासून सुरुवात करूया. घटकांच्या कनेक्शन बिंदूला काही परिमाणाचा विद्युत प्रवाह पुरवला जातो. ते सर्व कंडक्टरमधून वाहते, वेगळे करते. यावरून आपण असा निष्कर्ष काढतो की विभागातील एकूण प्रवाह प्रत्येक घटकातील विद्युत् प्रवाहाच्या बेरजेइतका आहे: I = I1 + I2 + I3.

आता व्होल्टेजसाठी. जर व्होल्टेज हे चार्ज हलवण्याचे काम असेल, तर एक चार्ज हलविण्यासाठी आवश्यक असलेले काम कोणत्याही घटकावर सारखेच असेल. म्हणजेच, प्रत्येक समांतर जोडलेल्या घटकावरील व्होल्टेज समान असेल. U=U1=U2=U3. साखळी विभागासाठी ओमच्या कायद्याच्या स्पष्टीकरणाच्या बाबतीत जितके मजेदार आणि दृश्यमान नाही, परंतु आपण समजू शकता.

समांतर कनेक्शनसाठी कायदे

प्रतिकारासाठी, गोष्टी थोड्या अधिक क्लिष्ट आहेत. चला चालकतेची संकल्पना ओळखू या. हे एक वैशिष्ट्य आहे जे सूचित करते की या कंडक्टरमधून चार्ज करणे किती सोपे किंवा कठीण आहे. हे स्पष्ट आहे की प्रतिकार जितका कमी असेल तितका प्रवाह जाणे सोपे होईल. म्हणून, चालकता - जी - ची प्रतिकारशक्तीच्या परस्पर म्हणून गणना केली जाते. सूत्रामध्ये, ते असे दिसते: G = 1/R.

आम्ही चालकता बद्दल का बोलत आहोत? कारण घटकांचे समांतर कनेक्शन असलेल्या विभागाची एकूण चालकता प्रत्येक विभागाच्या चालकतेच्या बेरजेइतकी असते. G = G1 + G2 + G3 - समजण्यास सोपे. समांतर घटकांच्या या नोडवर विद्युतप्रवाह किती सहजतेने मात करेल हे प्रत्येक घटकाच्या चालकतेवर अवलंबून असते. त्यामुळे ते दुमडणे आवश्यक आहे की बाहेर वळते.

आता आपण प्रतिकाराकडे जाऊ शकतो.चालकता ही प्रतिकाराची परस्परसंबंधित असल्याने, आम्हाला खालील सूत्र मिळू शकते: 1/R = 1/R1 + 1/R2 + 1/R3.

आम्हाला समांतर आणि अनुक्रमिक कनेक्शन काय देते?

सैद्धांतिक ज्ञान चांगले आहे, परंतु व्यवहारात ते कसे लागू करावे? कोणत्याही प्रकारचे घटक समांतर आणि मालिकेत जोडले जाऊ शकतात. परंतु आम्ही रेखीय घटकांचे वर्णन करणारी फक्त सर्वात सोपी सूत्रे मानली. रेखीय घटक हे प्रतिरोधक असतात, ज्यांना "प्रतिरोधक" देखील म्हणतात. तर तुम्ही जे शिकलात ते तुम्ही कसे वापरू शकता ते येथे आहे:

मोठ्या-मूल्याचे कोणतेही प्रतिरोधक उपलब्ध नसल्यास, परंतु अनेक लहान आहेत, तर अनेक प्रतिरोधकांना मालिकेत जोडून इच्छित प्रतिकार मिळवता येतो. जसे आपण पाहू शकता, हे एक उपयुक्त तंत्र आहे.
बॅटरीचे आयुष्य वाढवण्यासाठी, ते समांतर कनेक्ट केले जाऊ शकतात. या प्रकरणात व्होल्टेज, ओमच्या कायद्यानुसार, समान राहील (आपण मल्टीमीटरने व्होल्टेज मोजून खात्री करू शकता). आणि दुहेरी बॅटरीचा "आयुष्यकाळ" दोन घटकांपेक्षा खूप मोठा असेल जे एकमेकांना पुनर्स्थित करतील

फक्त लक्षात ठेवा: समान क्षमतेसह फक्त वीज पुरवठा समांतर जोडला जाऊ शकतो. म्हणजेच, मृत आणि नवीन बॅटरी कनेक्ट केली जाऊ शकत नाही.

तुम्ही तरीही कनेक्ट केल्यास, जास्त चार्ज असलेली बॅटरी कमी चार्ज केलेली बॅटरी चार्ज करेल. परिणामी, त्यांचे एकूण शुल्क कमी मूल्यावर जाईल.

सर्वसाधारणपणे, या संयुगेसाठी हे सर्वात सामान्य उपयोग आहेत.

आदर्श EMF स्रोत

इलेक्ट्रोमोटिव्ह फोर्स (ई) हे एक भौतिक प्रमाण आहे जे चार्ज वाहकांच्या बंद सर्किटमध्ये हालचालींवर बाह्य शक्तींच्या प्रभावाची डिग्री निर्धारित करते. दुस-या शब्दात, कंडक्टरमधून विद्युत् प्रवाह किती जोरदारपणे वाहतो हे EMF वर अवलंबून असेल.

अशा अनाकलनीय घटनांचे स्पष्टीकरण देताना, घरगुती शाळेतील शिक्षकांना हायड्रॉलिक सादृश्यांच्या पद्धतीकडे वळणे आवडते. जर कंडक्टर एक पाईप असेल आणि विद्युत प्रवाह म्हणजे त्यातून वाहणाऱ्या पाण्याचे प्रमाण असेल, तर EMF म्हणजे द्रव पंप करण्यासाठी पंप विकसित होणारा दबाव.

इलेक्ट्रोमोटिव्ह फोर्स हा शब्द व्होल्टेजसारख्या संकल्पनेशी संबंधित आहे. ती, ईएमएफ, व्होल्टमध्ये देखील मोजली जाते (युनिट - "व्ही"). प्रत्येक उर्जा स्त्रोत, मग ती बॅटरी असो, जनरेटर असो किंवा सौर पॅनेल असो, त्याची स्वतःची इलेक्ट्रोमोटिव्ह शक्ती असते. बहुतेकदा हा ईएमएफ आउटपुट व्होल्टेज (यू) च्या जवळ असतो, परंतु नेहमी त्यापेक्षा थोडा कमी असतो. हे स्त्रोताच्या अंतर्गत प्रतिकारामुळे होते, ज्यावर व्होल्टेजचा भाग अपरिहार्यपणे खाली येतो.

या कारणास्तव, ईएमएफचा आदर्श स्त्रोत त्याऐवजी एक अमूर्त संकल्पना किंवा वास्तविक जगात कोणतेही स्थान नसलेले भौतिक मॉडेल आहे, कारण बॅटरी रिनचा अंतर्गत प्रतिकार, जरी खूप कमी असला तरीही, पूर्ण शून्यापेक्षा वेगळा आहे.

ईएमएफचा आदर्श आणि वास्तविक स्रोत

विभेदक स्वरूपात

सूत्र बहुधा विभेदक स्वरूपात सादर केले जाते, कारण कंडक्टर सामान्यतः एकसंध नसतो आणि त्याला शक्य तितक्या लहान विभागांमध्ये विभागणे आवश्यक असते. त्यातून जाणारा विद्युत् प्रवाह परिमाण आणि दिशेशी संबंधित आहे, म्हणून ते स्केलर प्रमाण मानले जाते. जेव्हा जेव्हा वायरमधून परिणामी प्रवाह शोधायचा असतो तेव्हा सर्व वैयक्तिक प्रवाहांची बीजगणितीय बेरीज घेतली जाते. हा नियम केवळ स्केलर परिमाणांवर लागू असल्याने, वर्तमान देखील स्केलर प्रमाण म्हणून घेतले जाते. हे ज्ञात आहे की वर्तमान dI = jdS विभागातून जातो. त्यावरील व्होल्टेज एडीएल आहे, नंतर स्थिर क्रॉस सेक्शन आणि समान लांबी असलेल्या वायरसाठी, गुणोत्तर खरे असेल:

विभेदक फॉर्म

म्हणून, सदिश स्वरूपात विद्युत् प्रवाहाची अभिव्यक्ती असेल: j = E.

महत्वाचे! मेटॅलिक कंडक्टरच्या बाबतीत, वाढत्या तापमानासह चालकता कमी होते, तर सेमीकंडक्टरसाठी ती वाढते. ओमोव्हचा कायदा कठोर आनुपातिकता दर्शवत नाही

निरपेक्ष शून्याच्या जवळ असलेल्या तापमानात धातू आणि मिश्रधातूंच्या मोठ्या गटाचा प्रतिकार नाहीसा होतो आणि या प्रक्रियेला सुपरकंडक्टिव्हिटी म्हणतात.